Equirectangular image (등장방형 이미지)
Equirectangular image는 구면 좌표계를 직각 좌표계로 매핑한 이미지입로 구면 좌표계의 각도를 직각 좌표계의 픽셀로 일대일 매핑하여 표현한다.
구면 좌표계에서는 위도(latitude)와 경도(longitude)로 이미지를 표현하는데, 위도는 구의 수평 방향을 나타내며, -90에서 90도까지의 범위를 가지고 경도는 구의 수직 방향을 나타내며, -180에서 180도까지의 범위를 가진다. Equirectangular 이미지는 이러한 구면 좌표계를 사용하여 이미지를 표현한다. 이미지의 너비는 360도의 경도 범위에 매핑되고, 높이는 -90에서 90도의 위도 범위에 매핑된다. 따라서 이미지의 크기는 경도와 위도의 해상도에 따라 결정된다.
이러한 Equirectangular 이미지는 주로 360도 동영상, 가상 현실(VR) 이미지, 행성 표면 이미지 등과 같은 구형 데이터를 표현하는 데 사용되는데, 이러한 이미지는 구면 좌표계의 특성을 보존하면서도 직각 좌표계에서의 이미지 처리 및 분석을 가능하게 한다.


구면좌표계 변환

Equirectangular image는 가로(x) 360도, 세로(y) 180도의 범위를 가지기 때문에 구면 좌표계로 변환할 수 있다.
이미지 좌표를 0~1 사이로 정규화하고 위도(latitude)와 경도(longtitude)를 위와 같이 계산하면 된다.
구면 좌표까지의 3D 벡터

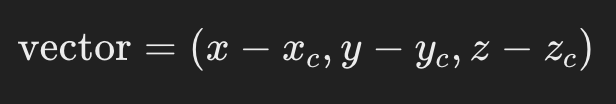
카메라 중심에서 구면 좌표 지점까지의 3D 벡터를 계산할 수 있는데, 위와 같이 직각좌표계 좌표(x, y, z)를 구하고 벡터를 계산할 수 있다.
import numpy as np
def image_to_spherical_coordinates(x_image, y_image, image_width, image_height):
# Normalize image coordinates to the range [0, 1]
x_normalized = x_image / (image_width - 1)
y_normalized = y_image / (image_height - 1)
# Calculate latitude (elevation) and longitude (azimuth) from normalized image coordinates
phi = np.pi * y_normalized
theta = 2 * np.pi * x_normalized
return phi, theta
def spherical_to_cartesian(phi, theta, r):
x = r * np.sin(phi) * np.cos(theta)
y = r * np.sin(phi) * np.sin(theta)
z = r * np.cos(phi)
return np.array([x, y, z])
def relative_vector_from_image_coordinates(x_image, y_image, image_width, image_height, camera_center, radius):
# Convert image coordinates to spherical coordinates
phi, theta = image_to_spherical_coordinates(x_image, y_image, image_width, image_height)
# Convert spherical coordinates to Cartesian coordinates
vector = spherical_to_cartesian(phi, theta, radius)
# Calculate relative vector from camera center to the point
relative_vector = vector - camera_center
return relative_vector
# Example inputs
x_image = 100 # Example image x-coordinate
y_image = 50 # Example image y-coordinate
image_width = 800 # Example image width
image_height = 600 # Example image height
camera_center = np.array([0, 0, 0]) # Example camera center
radius = 1 # Example radius
# Calculate the relative vector
relative_vector = relative_vector_from_image_coordinates(x_image, y_image, image_width, image_height, camera_center, radius)
print("Relative vector:", relative_vector)
카메라 roll & pitch & yaw를 이용한 절대 좌표 벡터 변환
현재까지 계산한 벡터는 이미지 기준으로 계산한 상대 좌표 벡터이다. 때문에 절대 좌표 벡터를 얻기 위해서는 카메라 회전 각도인 roll, pitch, yaw를 이용하여 구면 좌표상의 벡터를 회전해야 한다.
import numpy as np
from scipy.spatial.transform import Rotation
def spherical_to_cartesian(phi, theta, r):
x = r * np.sin(phi) * np.cos(theta)
y = r * np.sin(phi) * np.sin(theta)
z = r * np.cos(phi)
return np.array([x, y, z])
def absolute_vector_from_spherical(phi, theta, r, camera_center, roll, pitch, yaw):
# Convert spherical coordinates to Cartesian coordinates
vector = spherical_to_cartesian(phi, theta, r)
# Create a rotation object using Euler angles (roll, pitch, yaw)
r = Rotation.from_euler('xyz', [roll, pitch, yaw], degrees=True)
# Rotate the vector
rotated_vector = r.apply(vector)
# Translate the rotated vector to the camera center
absolute_vector = rotated_vector + camera_center
return absolute_vector
# Example inputs
phi = np.pi/4 # Example elevation
theta = np.pi/4 # Example azimuth
r = 1 # Example radius
camera_center = np.array([0, 0, 0]) # Example camera center
roll = 30 # Example roll angle in degrees
pitch = 45 # Example pitch angle in degrees
yaw = 60 # Example yaw angle in degrees
# Calculate the absolute vector
absolute_vector = absolute_vector_from_spherical(phi, theta, r, camera_center, roll, pitch, yaw)
print("Absolute vector:", absolute_vector)'📖 Fundamentals > Computer Vision' 카테고리의 다른 글
| [객체 검출] 앵커 박스(Anchor Box)란 무엇인가? | 객체 검출 모델에서의 역할과 한계 (0) | 2024.08.10 |
|---|---|
| 직각좌표계 & 구면좌표계 | 좌표 변환 (0) | 2024.03.29 |
| [객체 검출] RPN이 무엇일까? | 객체 검출에서 후보 영역을 생성하는 네트워크 | Region Proposal Network 설명 (3) | 2023.11.25 |
| [객체 검출] NMS가 무엇일까? | 객체 검출에서 겹치는 bbox를 제거하는 방법 | Non-Maximum Suppression 설명 (1) | 2023.11.25 |
| Computer Vision (컴퓨터 비전) 이 무엇일까 !? (1) | 2023.04.07 |