반응형
직각 좌표계와 구면 좌표계는 이미지 처리 및 분석에서 사용되는 좌표 시스템이다.
직각 좌표계(Rectangular Coordinates)
- 이미지를 다룰 때 가장 일반적으로 사용되는 좌표 시스템
- 이미지는 픽셀로 구성되어 있으며, 각 픽셀은 행(row)과 열(column)의 인덱스로 표현
- 일반적으로 왼쪽 상단 모서리가 (0, 0)으로 시작하여 오른쪽으로 갈수록 열(column)이 증가하고 아래로 갈수록 행(row)이 증가
구면 좌표계(Spherical Coordinates)

- 구면 좌표계는 이미지 처리에서 주로 사용되지는 않지만, 컴퓨터 비전의 특정 분야에서 사용될 수 있음
- 주로 3D 공간에서 사용되며, 위도(latitude), 경도(longitude), 고도(altitude)와 같은 좌표를 사용하여 지구 표면을 나타냄
- 회전 및 방향을 다루는 데 유용하며, 카메라의 위치 및 방향을 정확하게 추적하는 데 사용될 수 있음
- 예를 들어, 이미지의 특징점을 감지하고 추적하는 작업에서는 직각 좌표계가 주로 사용되지만, 3D 객체의 위치 및 방향을 추정하는 작업에서는 구면 좌표계가 사용될 수 있음
직각좌표계 → 구면좌표계 좌표 변환
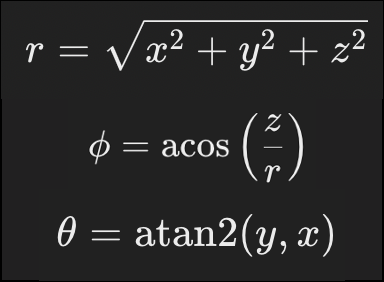
구면좌표계 → 직각좌표계 좌표 변환
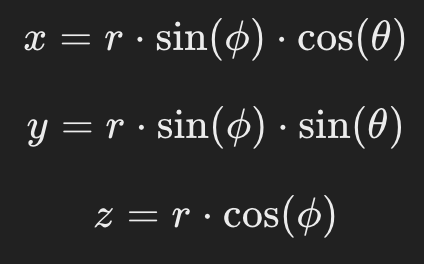
코드 예시
import math
# 직각 좌표계에서 구면 좌표계로 변환하는 함수
def rectangular_to_spherical(x, y, z):
# 구의 반지름 계산
r = math.sqrt(x**2 + y**2 + z**2)
# 위도 계산
phi = math.acos(z / r)
# 경도 계산
theta = math.atan2(y, x)
return phi, theta
# 구면 좌표계에서 직각 좌표계로 변환하는 함수
def spherical_to_rectangular(phi, theta, r):
# 직각 좌표 x, y, z 계산
x = r * math.sin(phi) * math.cos(theta)
y = r * math.sin(phi) * math.sin(theta)
z = r * math.cos(phi)
return x, y, z
# 예시: 직각 좌표 (1, 1, 1)를 구면 좌표로 변환
rectangular_x = 1
rectangular_y = 1
rectangular_z = 1
phi, theta = rectangular_to_spherical(rectangular_x, rectangular_y, rectangular_z)
print("구면 좌표 (phi, theta):", phi, theta)
# 예시: 구면 좌표 (pi/4, pi/4)를 직각 좌표로 변환
spherical_phi = math.pi / 4 # 45도
spherical_theta = math.pi / 4 # 45도
radius = 1 # 예시로 반지름을 1로 가정
x, y, z = spherical_to_rectangular(spherical_phi, spherical_theta, radius)
print("직각 좌표 (x, y, z):", x, y, z)반응형
'📖 Fundamentals > Computer Vision' 카테고리의 다른 글
| [객체 검출] 앵커 박스(Anchor Box)란 무엇인가? | 객체 검출 모델에서의 역할과 한계 (0) | 2024.08.10 |
|---|---|
| Equirectangular Image (등장방형 이미지) 설명 | 이미지 좌표 변환 | 구면좌표 벡터 계산 (0) | 2024.03.29 |
| [객체 검출] RPN이 무엇일까? | 객체 검출에서 후보 영역을 생성하는 네트워크 | Region Proposal Network 설명 (3) | 2023.11.25 |
| [객체 검출] NMS가 무엇일까? | 객체 검출에서 겹치는 bbox를 제거하는 방법 | Non-Maximum Suppression 설명 (0) | 2023.11.25 |
| Computer Vision (컴퓨터 비전) 이 무엇일까 !? (1) | 2023.04.07 |